1. Linear Equations are recognized because:
a. The equations have an x and y variable
b. The constant within the equation is one
c. the highest power of the variables are each one
d. none of the above
2. Slope-Intercept Format would be:
a. y = mx + b
b. ax + by = y
c. y + b = mx
d. ax + by + c = 0
3. The slope of a line is defined as:
a. the horizontal change in x divided by the vertical change in y
b. the vertical change in y divided by the horizontal change in x
c. the ratio of run to the rise
d. being constant with no vertical change
4. Given the equation: 3x + 2y = 10, the slope of the line and y intercept of this equation would be:
a. slope = 3; y intercept = 10
b. slope = -3; y intercept = 5
c. slope = -3/2 ; y intercept = 5
d. slope = -2/3 ; y intercept = 2
5. Given the system of equations, solve this system, if a solution exists:
x + y – z = 2
3x + y – z = -2
4x – 2y + z = -13
a. (-2, 1, -3)
b. (1, 2, -3)
c. (2, -1, 5)
d. there is no solution to this system of equations
6. Given the system of equations, solve this system, if a solution exists:
5x – 4y = 9
x = 2y – 3
a. no solution
b. (5, 4)
c. (1, -3)
d. (-1, 3)
7. Given the relation, z, of ordered pairs:
z = {(john, rangers game), (lee, rangers game), (john, stars game)}
a. these ordered pairs of relation z represent a function
b. these ordered pairs of relation z represent a dependent function
c. these ordered pairs of relation z do not represent a function
d. none of the above
8. The domain of the function, f (x) = 2x -5 is:
a. all Real numbers except for x = ½
b. all Real numbers except for x = 5
c. all Real numbers except x = 0
d. all Real numbers, with no exceptions
9. Given the function, f (x) = -3x/2 + 4, evaluate f (x – a):
a. -3x – a + 4
b. -3x -3a + 4
c. (-3x + 3a)/2 + 4
d. (-3x – 3a)/2 + 2
10. The composition of two functions, f (x) and g (x) is defined as:
a. f [ f (x) ] g (x)
b. f [ g(x) ]
c. g [ g (x) ] g (x)
d. f (x) · g (x)
11. Given: f (x) = 4x – 3, g (x) = 5x 2 – 2; Find: f ◦ g
a. 9x 2 – 2
b. 20x 2 -11
c. 8x 2 – 3
d. none of the above
12. The Supply and Demand functions for the production of an electronic toy is:
S (x) = x2 + 10x + 20
D (x) = 28 + 12x
Find the market equilibrium price point in dollars.
a. -4
b. 2
c. 4
d. -2
13. If a product is sold for less than the supply = demand price point,
there may be a:
a. surplus, and demand may cause the price to increase
b. surplus, and demand may cause the price to decrease
c. shortage, and the demand may cause the price to increase
d. shortage, and the demand may cause the price to decrease
14. Given: f (x) = 1/x , g (x) = x ; Find: f ◦ g
a. x
b. 1/x
c. x 2
d. none of the above
15. If the inverse of a function exists, then the following would be true:
a. f -1 ◦ f = 1
b. f -1 ◦ f = x
c. f -1 ◦ g = x
d. f -1 ◦ g = 1
16. If the inverse of a function exists, when the function and its inverse are both drawn on the same graph, the following will occur:
a. the graphs of the function and its inverse will cross each other
b. the graphs of the function and its inverse will be parallel
c. the graphs of the function and its inverse will be a mirror image of each other about the line y = x.
d. the graphs of the function and its inverse will be a mirror image
e. of each other about the y axis
17. Given: f (x) = x – 3 ; Find: f -1
a. x – y
b. y – 3
c. x + 3
d. none of the above
18. Given: f (x) = 2/(x – 3) , g( x) = 2/x + 3
Are these two functions inverses of each other?
a. yes
b. no
c. the inverses do not exist in this case
d. none of the above
19. Evaluate the following limit:
lim x –> ∞ (x3 – 2x + 5)/(2x3 – 7)
a. 0
b. ½
c. -1
d. limit does not exist
20. The derivative of the function f, at x, is known as:
a. the point at which the function is discontinuous
b. the rate of change of the function f, at x
c. the point at x where the tangent line is at a slope of one
d. none of the above
21. Given: f (x) = (-1/3)x2 + 7x – 2 . The derivative of f with respect to x is:
a. (-2/3)x + 7
b. (-2/9)x + 7
c. (-1/3)x – 2
d. none of the above
22. Given: z = f (x, y) = x 2 + y2 + xy – 5
Find partial derivatives f x and f y of the given function.
a. f x (x, y) = 2y + 2x ; f y (x, y) = 2x + 2y
b. f x (x, y) = 2x ; f y (x, y) = 2y
c. f x (x, y) = 2x + y ; f y (x, y) = 2y + x
d. f x (x, y) = 2 + x ; f y (x, y) = 2 + y
23. Given: z = f (x, y) = x2 + 3xy – 4y2
Find partial derivatives f x and f y of the given function.
a. f x (x, y) = 2x + 3y ; f y (x, y) = 3x – 8y
b. f x (x, y) = 3y + 8y2 ; f y (x, y) = 2x + y
c. f x (x, y) = 2y + x ; f y (x, y) = 3x + y
d. f x (x, y) = 2y + x ; f y (x, y) = 2x + 4y
24. Given: z = f (x, y) = (3y)/(2x)
Find partial derivatives f x and f y of the given function.
a. f x (x, y) = – 3y/2x 2 ; f y (x, y) = 3/2x
b. f x (x, y) = -3y/2x ; f y (x, y) = 2x
c. f x (x, y) = – 3y/2x ; f y (x, y) = 3/x
d. none of the above
25. The “first derivative test” will help determine if a point on the graph of
the function y = f (x) :
a. has a tangent line with a slope of one
b. has a relative maximum or minimum point
c. has a tangent line with a slope of negative one
d. none of the above
26. Given the function: f (x, y) = xy 2
Subject to the constraint function of x + y = 5
The Lagrange Function would then be equal to:
a. (x + y)5λ + xy 2
b. (xy2) λ
c. (xy2) + λ(x + y – 5)
d. (xy2 + y) λ
27. Find: ∫ (3x2 – 7x + 2) dx
a. 6x3 – (7/2)x2 + 2x + C
b. x 3 – (7/2)x 2 + 2x + C
c. 6x3 – 7 + C
d. none of the above
28. Find : ∫ [(1/x 2) – 2x -1] dx
a. -x-1 – 2 | ln x | + C
b. -x – 2 | ln x | + C
c. – 2 | ln x | + C
d. none of the above
29. Given: z = f (x, y) = x 2 – y 2 + xy – 5
Find ∂z/∂x and ∂z/∂y:
a. f x (x, y) = 2x + y ; f y (x, y) = -2y + x
b. f x (x, y) = 2x +2 x ; f y (x, y) = 2y + y
c. f x (x, y) = x + 2x ; f y (x, y) = 2y + x
d. f x (x, y) = 2x + y ; f y (x, y) = 2y + y
30. Evaluate: 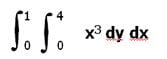
a. 1
b. -2
c. -1
d. 0